Schwarze Löcher – gibt es sie wirklich und wie können wir das wissen?

Schwarze Löcher gehören zu den faszinierendsten Objekten im Universum. Aber wie können wir eigentlich wissen, dass es sie überhaupt gibt?

Schwarze Löcher faszinieren seit sie vor mehr als 100 Jahren erstmals vorgeschlagen wurden. Einstein, dessen Allgemeine Relativitätstheorie ihre Grundlage bildet, glaubte nicht an sie, aber wir haben heute eindeutige Hinweise, die kaum einen anderen Schluss zulassen, als dass es diese seltsamen Objekte wirklich gibt. In diesem Artikel möchte ich darlegen, warum Astronomen sie für real halten.

Die finsteren Schwerkraftmonster

Sie sollen zu tausenden als Zombies explodierter Riesensterne durch die Milchstraße geistern und alles verschlingen, das ihnen zu nahe kommt. Wer das Pech hat, einem Schwarzen Loch in die Quere zu kommen, wird von ihm zu einer Spaghettinudel auseinandergezogen und verschwindet auf Nimmerwiedersehen hinter dem Ereignishorizont. Es gibt sie in kleiner und sehr großer Ausführung mit kaum etwas dazwischen, und bei den ganz großen würde die Spaghettifizierung erst tief in ihrem Inneren stattfinden. In ihnen sollen Zeit und Raum die Rollen vertauschen und man könnte in ihnen rückwärts durch die Zeit reisen. In ihrem Zentrum verbirgt sich ein Punkt unendlicher Dichte oder vielleicht ein komplettes Universum – es ranken sich regelrechte Mythen um Schwarze Löcher.

Richtig ist, dass die meisten von ihnen als Reste von Supernova-Explosionen verbleiben, allerdings muss ein Stern wenigstens 25 bis 30 Sonnenmassen an Startmasse auf die Waage bringen, damit er nicht lediglich als Neutronenstern endet, und solche Sterne sind extrem selten, weniger als 0,01% der Sterne sind so massereich. Die Chance, dass dem Sonnensystem so ein Objekt irgendwann zufällig über den Weg läuft, ist astronomisch klein. Klein sind auch die Abmessungen eines Schwarzen Lochs; die Spaghettifizierung würde tatsächlich stattfinden, wenn man einem stellaren Schwarzen Loch auf ein paar Kilometer nahe käme: dort nimmt die Schwerkraft über den Radius so schnell zu, dass die Kraft, die an den Füßen zieht, viel stärker wäre als diejenige, die auf den Kopf wirkt, was einen letztendlich zerreißen müsste.

Allerdings muss man ihnen dazu extrem nahe kommen – wären sie normale Sterne, dann wäre man in dieser Entfernung von ihrem Zentrum genau so tot, weil man sich bereits tief in ihrem Kern befände. Weiter entfernt ist ihre Schwerkraftwirkung dieselbe wie die jedes anderen Sterns der entsprechenden Masse. Schwarze Löcher sind daher keine Staubsauger, die alles in Reichweite ansaugen und verschlingen; man könnte sie in ein paar Millionen Kilometern Entfernung Milliarden Jahre lang umkreisen, wie jeden anderen Stern auch. Ihre Schwerkraft wird nur deshalb in ihrer unmittelbaren Nähe so hoch, weil sehr viel Masse auf sehr kleinem Raum konzentriert ist.

Auf der anderen Seite gibt es supermassereiche Schwarze Löcher, die Millionen bis Milliarden Sonnenmassen aufbringen. Sie finden sich im Zentrum so gut wie jeder Galaxie und skalieren mit der Größe der Galaxie, so dass man davon ausgeht, dass sie mit den Galaxien zusammen entstehen (der genaue Mechanismus ist aber noch offen). Bei ihnen ist alles sehr viel größer, etwa in der Größenordnung von mehreren Sonnendurchmessern bis über die Größe des Sonnensystems hinaus. Auch der Radius, über den die Schwerkraft zunimmt, und so könnte man ohne viel zu bemerken und vor allem ohne spaghettifiziert zu werden in ein solches hinein fallen. Allerdings hätte man nach Passage des Ereignishorizonts keine Chance, es sich noch einmal anders zu überlegen und umzukehren.

Die Raumzeit fließt am Ereignishorizont gewissermaßen wie ein Wasserfall mit Lichtgeschwindigkeit in das Schwarze Loch hinein, und da sich nichts so schnell wie das Licht bewegen kann, hat man spätestens am Ereignishorizont verloren – von da ab gibt es nur eine Richtung: zum Zentrum hin, so wie die Zeit nur eine Richtung in die Zukunft kennt. Kurz vor dem Erreichen desselben wird man aber auch in einem supermassereichen Schwarzen Loch spaghettifiziert, man hat nur vorher die Gelegenheit, hinter sich das Weltall blauverschoben zu einem Tunnel zusammenschrumpfen zu sehen und dabei in die Zukunft schauen zu können; was den Nachteil hat, dass einen alles Licht, das noch ins Schwarze Loch fällt, grillen würde, weil die Zeit draußen zunehmend schneller verläuft. Falls man nicht schon gleich hinter dem Horizont in Hawkings Feuerwand fällt, aber wer weiß das schon…

Grande Finale

Die Entstehung eines stellaren Schwarzen Lochs geschieht durch den Kernkollaps am Ende des Lebens eines sehr massereichen Sterns. In Sternen besteht ein Gleichgewicht zwischen dem Gewichtsdruck des Gases und dem Druck der bei der Fusion im Kern entstehenden Strahlung. Zu Beginn findet in einem kleinen, nur etwa erdgroßen Bereich die Kernfusion von Wasserstoff zu Helium statt. Da es keinen Austausch mit der Materie drumherum gibt, wird der Wasserstoff immer weniger und der Strahlungsdruck lässt nach, so dass der Stern zusammensackt und so Druck und Temperatur erhöht. Die Fusion verlagert sich somit weiter nach außen in eine Schale und der Stern wird ob des größeren an der Fusion beteiligten Volumens heller und heißer, was ihn äußerlich aufbläht. Bei steigendem Druck und Temperatur zündet dann irgendwann auch die Heliumfusion und produziert Kohlenstoff und Beryllium.

Auch das Heliumbrennen wandert irgendwann in eine Schale aus und so baut sich allmählich eine Zwiebelstruktur auf. Die letzte Stufe ist das nur einen Tag dauernde Brennen von Silizium, bei dem zahlreiche Kerne bis hinauf zum Eisen entstehen. Alle Fusionsphasen bis hierher haben Energie erzeugt und stabilisierenden Strahlungsdruck geliefert. Das ist nicht mehr der Fall, wenn Eisenatome beginnen, andere Kerne anzulagern, diese verbrauchen dafür Energie und kühlen das Innere des Sterns rasch ab, was den Strahlungsdruck zum Erliegen bringt.

Wo bei einem Weißen Zwerg die Elektronen zwischen den Atomen noch einen sogenannten Entartungsdruck aufbringen, da sie nach dem Pauli-Prinzip nicht den gleichen Raum im gleichen Quantenzustand bevölkern können und weil die Zahl der Quantenzustände begrenzt ist, ist der Gewichtsdruck in einem Stern von mehr als 10 Sonnenmassen groß genug, sie einfach in die Atomkerne hineinzuquetschen, wo sie sich mit den Protonen unter Freisetzung einer immensen Zahl von Neutrinos zu Neutronen vereinigen, die sich bedeutend dichter packen lassen.

Der Kern des Sterns kollabiert daraufhin im freien Fall zu einer weniger als 30 km durchmessenden Kugel und setzt dabei so viele Neutrinos frei, dass diese dem von außen in den Hohlraum einbrechenden Gas noch einen letzten Widerstand entgegensetzen können und es aufheizen, bis eine den Stern nach außen durchlaufende Druckwelle überall die nukleare Fusion zündet, die ihn in einer gewaltigen Explosion zerreißt.

Doch es verbleibt genug Materie in der Nähe des gerade entstandenen Neutronensterns, die nun auf ihn herabstürzt und ihn über die Kante stößt. Denn oberhalb einer bestimmten Masse, die irgendwo zwischen 2,1 und 3 Sonnenmassen liegt, kann auch ein Neutronenstern seinen eigenen Gewichtsdruck nicht mehr tragen. Die Physiker Tolman, Oppenheimer und Volkoff haben 1939 ausgerechnet, dass oberhalb der nach ihnen benannten Tolman-Oppenheimer-Volkoff-Grenze (TOV-Grenze) der Neutronenstern nicht mehr stabil sein kann, weil die Teilchen alle quantenmechanischen Energieniveaus besetzt haben (ähnlich wie die Elektronen an der bekannteren Chandrasekhar-Grenze zwischen Weißen Zwergen und Neutronensternen), was ihrem maximal möglichen Gegendruck eine Obergrenze setzt.

Darüber hinaus ist keine Kraft bekannt, die der Schwerkraft noch Paroli bieten könnte – und der Neutronenstern stürzt zu einer Punktmasse in sich zusammen, die hinter einem Ereignishorizont verschwindet, an dem die Zeit scheinbar zum Stillstand kommt, an dem der Schwerkraft nichts mehr entkommen kann, kein Licht, nicht einmal die Kausalität selbst – ein Schwarzes Loch.

So behauptet es jedenfalls die moderne Astrophysik. Aber wie kann sie Aussagen über Bedingungen machen, die in keinem Labor der Welt reproduziert oder erforscht werden können? Gilt Physik nicht immer nur in den Grenzen, in denen sie durch Messungen oder Beobachtungen verifiziert werden kann? Gibt es am Ende vielleicht gar keine Schwarzen Löcher?

Schwarze Löcher – gibt es sie wirklich und wie können wir das wissen?Dunkle Sterne und krumme Raumzeiten

Einstein selbst glaubte jedenfalls nicht an sie. Obwohl der Begriff erst 1960, fünf Jahre nach seinem Tod, geprägt wurde, ist die Idee der dunklen Sterne schon viel älter, älter noch als die Relativitätstheorie selbst, die ihrem heutigen Modell zugrunde liegt. Schon 1784 veröffentlichte der britische Astronom und Kleriker John Michell eine Berechnung, dass ein Objekt mit 500 Sonnendurchmessern und durchgehend der gleichen Dichte wie die Sonne nach Newtons Gravitationsgesetz eine Fluchtgeschwindigkeit an der Oberfläche haben würde, die der Lichtgeschwindigkeit entspräche, womit ihm kein Licht entkommen könnte – ein „Dunkler Stern“, wie Michell dieses hypothetische Objekt nannte.

1915 entwickelte Albert Einstein aus den Postulaten, dass die Lichtgeschwindigkeit in allen Bezugssystemen gleich groß ist (eine durch Messungen bestätigte Beobachtung) und der Gleichwertigkeit von Beschleunigung und Gravitation seine Allgemeine Relativitätstheorie (ART), der zufolge eine Masse Raum und Zeit um sich herum krümmt. Dies wird gerne qualitativ durch ein Gummituch versinnbildlicht, auf welches man ein Gewicht legt, welches das Tuch eindellt. Kein wirklich gelungenes Bild, denn schließlich ist es die echte Schwerkraft, die das Tuch eindellt, und zwar in eine höhere (im Falle des Tuchs die dritte) Dimension, wobei das zweidimensionale Tuch für unseren dreidimensionalen Raum stehen soll.

Lässt man Murmeln über die Oberfläche des Tuchs laufen, rollen sie auf Bahnen um das Gewicht herum, die denen von Keplerorbits ähneln, was aber weniger an dem eingedellten Tuch, sondern vor allem an der Schwerkraft der Erde liegt, die sie in die Vertiefung rollen lässt, die sie aber dank der Fliehkraft auf der gekrümmten Tuchoberfläche meiden können. Das eingedellte Tuch legt außerdem eine vierte Raumdimension in der ART nahe, in die sich der Raum krümmt, aber eine solche Dimension kommt in den Gleichungen der ART gar nicht vor, sondern nur die drei Raumdimensionen und die Zeit.

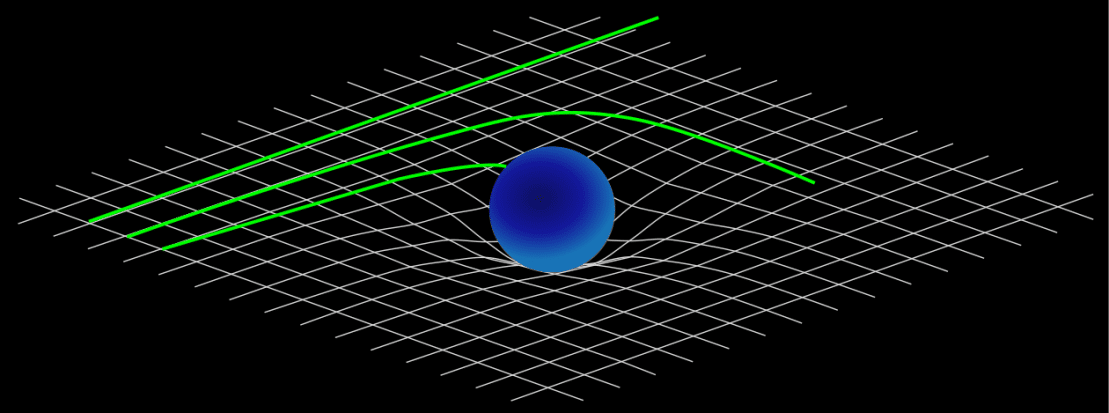
Tatsächlich verändert die Masse die Geometrie der Raumzeit um sich herum. So gilt zum Beispiel, dass der Umfang eines Kreises um eine Masse kleiner ist als 2·π mal seinem Radius, so wie es etwa auf einer Kugeloberfläche der Fall ist. Zum Beispiel misst der Äquator einer Kugel nur viermal den Abstand vom Pol zum Äquator, welcher dem Radius des Äquators entlang der Kugeloberfläche entspricht. Neben der Verzerrung der Raumgeometrie wird auch der Zeitverlauf in der Nähe einer Masse verzerrt: sie läuft umso langsamer, je näher man der Masse kommt („gravitative Zeitdilatation“).

Beide Effekte wurden durch zahlreiche Experimente bestätigt, etwa die Raumkrümmung anhand der Lichtablenkung im Schwerefeld, die die Position von Sternen in der Nähe der Sonne während der Sonnenfinsternis vom 29. Mai 1919 veränderten, das berühmte Experiment von Sir Arthur Eddington. Noch genauere Messungen gelangen mit Radioteleskopen, die exakt vermaßen, wie die Sonne die Position ferner Radioquellen bei ihrem Vorbeiziehen an diesen veränderte.

Den Effekt der Zeitdilatation im Schwerefeld wiesen wiederum Joseph C. Hafele und Richard E. Keating 1971 in einem berühmten Experiment nach, bei dem sie präzise Cäsium-Atomuhren in Linienjets um die Erde schickten und nachwiesen, dass die Uhren im Flugzeug schneller als auf der Erde verbliebene Referenzuhren gelaufen waren.

Schwerkraft ist nun nichts anderes als das Bestreben einer Masse oder eines Photons, den kürzesten Weg zwischen zwei Raumzeitpunkten durch die gekrümmte Raumzeit zu nehmen. Ein solcher Weg wird in der Sprache der Geometrie „Geodäte“ genannt (Schiffe und Flugzeuge bewegen sich bei Fernreisen, wenn möglich, auf Geodäten der Erde, das sind Abschnitte von Großkreisen, deren Mittelpunkt das Erdzentrum ist). Zu erläutern, wie genau vor allem durch die Zeitdilatation ein Steinwurf zu einer Parabel wird, würde hier zu weit führen, ist aber auf der Seite meines Scienceblogs-Kollegen Martin Bäker anschaulich anhand eines Beispiels erklärt.

Einstein formulierte die Allgemeine Relativitätstheorie in Form seiner „Feldgleichungen“, die die räumliche Verteilung von Masse / Energie (aber auch Druck oder dem Fluss von Masse / Energie, sowie weiteren Größen) in Beziehung zur resultierenden Raumzeitkrümmung setzen. Die Lösung der Gleichungen in geschlossener Form ist nur für bestimmte einfache Topologien möglich, und eine der einfachsten ist eine kugel- oder punktförmige Massenverteilung. Der Physiker Karl Schwarzschild fand schon wenige Monate nachdem Einstein seine Feldgleichungen veröffentlicht hatte, eine Lösung für diesen Fall. Und die besagte unter anderem, dass das Licht einer beliebigen (nicht rotierenden, nicht geladenen) Masse M, die auf einen Radius von weniger als r_s = 2GM/c² (ihrem „Schwarzschildradius“) komprimiert ist, innerhalb dieses Radius nicht mehr entkommen kann – der Ereignishorizont für ein nichtrotierendes, nicht geladenes Schwarzes Loch. G ist hierbei die Gravitationskonstante (6,6743·10^-11 m³/(kg·s²)).

Mit der Masse M in Sonnenmassen M_Sonne wird die Gleichung einfacher: r_s = 2,95 km · M[M_Sonne]. Ein Objekt von drei Sonnenmassen hat also zum Beispiel einen Schwarzschildradius von knapp 9 km. Auch die Erde hat einen Schwarzschildradius, er beträgt 0,9 cm. Allerdings ist es schwer, die Erde in eine Kugel von 0,9 cm Radius zu quetschen. Wenn man dies allerdings schafft (oder wenn die Schwerkraft bei einem hinreichend schweren Stern dies erledigt), dann schrumpft die Masse gemäß der Schwarzschild-Lösung zu einem Punkt, der Singularität zusammen.

Bei rotierenden Schwarzen Löchern wird die Raumzeit insgesamt mitgezogen (auch dies wurde im Experiment im Schwerefeld der Erde nachgewiesen), deshalb kann man ein rotierendes Schwarzes Loch enger umkreisen und der Ereignishorizont ist hier nicht mit dem Schwarzschildradius identisch. Roy Kerr fand die Lösung für rotierende Schwarze Löcher 1963: hier ist die Singularität kein Punkt, sondern ein unendlich dünner Ring, der mit zunehmender Rotation wächst, während der Ereignishorizont schrumpft. Bei maximaler Rotation berührt die Ringsingularität den Ereignishorizont beim halben Schwarzschildradius (r_g = GM/c², auch „Gravitationsradius“ genannt), und die Raumzeit rotiert am Ereignishorizont mit Lichtgeschwindigkeit. Bei kleiner Rotation geht die Lösung in die von Schwarzschild über mit einer zum Punkt schrumpfenden Ringsingularität und einem Ereignishorizont bei r_s = 2 r_g.

Hart am Limit: Neutronensterne

Neutronensterne liegen mit ihren Radien schon in der Größenordnung ihres Schwarzschildradius. Aber – woher weiß man überhaupt, wie groß ein Neutronenstern ist? Diese Objekte sind viel zu klein, als dass man ihren Durchmesser direkt beobachten könnte, und so muss man ihre Radien indirekt bestimmen. Eine Möglichkeit sind Pulsare, bei denen es sich um rotierende Neutronensterne handelt, deren gegen die Rotationsachse verkipptes Magnetfeld bei jeder Umdrehung einen Radiopuls erzeugt. Aus der Pulsfrequenz kann man somit auf die Rotationsgeschwindigkeit schließen. Es lässt sich leicht ausrechnen, bei welcher Rotationsrate die Fliehkraft einen Neutronenstern zerreißen würde. Der am schnellsten rotierende Pulsar dreht sich 716 Mal pro Sekunde; wenn er 2 Sonnenmassen oder weniger hat, darf er demgemäß nicht mehr als 17 km Radius haben – dies ist als Obergrenze zu verstehen, er kann deutlich kleiner sein, nur keinesfalls größer.

Schwieriger und nur für Neutronensterne mit bekannten Entfernungen möglich – entweder für solche, die nahe genug sind, dass man ihre Parallaxe messen kann oder für solche, die sich in Sternhaufen bekannter Entfernung befinden – ist der Rückschluss auf ihren Durchmesser aus ihrer thermischen Röntgenleuchtkraft. Diese Leuchtkraft hängt, wie die aller Temperaturstrahler, von der Temperatur und der Größe ihrer Oberfläche ab. So bestimmt man auch die Durchmesser von Sternen, allerdings anhand ihrer Leuchtkraft im Sichtbaren und Infraroten. Die Temperatur lässt sich aus derjenigen Röntgenfrequenz bestimmen, bei der das Maximum der Ausstrahlung liegt. Aus der Entfernung und der beobachteten Helligkeit kann man auf die Leuchtkraft schließen und zusammen mit der Temperatur auf die Oberfläche und damit den Radius. Dabei muss jedoch im Unterschied zu Fixsternen die Zeitdilatation berücksichtigt werden, die sich auf die abgestrahlte Frequenz und Leistung auswirkt, und dafür braucht man die Masse. Bisher gelang es bei einem nahen Neutronenstern, RX J1856-4754, mit dieser Methode den Radius zu bestimmen, aber seine Masse ist unbekannt, da er keinen Stern umkreist. Die Masse von Neutronensternen kann man bei solchen im Orbit um Sterne bekannter Massen bestimmen, die sich wiederum aus den Eigenschaften des umkreisten Sterns ermitteln lässt. So bestimmte Pulsarmassen liegen alle zwischen 1,2 und 2,7 Sonnenmassen.

Für RX J1856-4754 kam man auf einen Radius von 11,4±1,1 km, wenn der Neutronenstern mit 1,4 Sonnenmassen an der unteren Massengrenze liegt, und auf 14,3±1 km, falls er an der oberen Grenze liegt. Für 8 Pulsare in Kugelsternhaufen fand man Durchmesser zwischen 9,5 und 13,7 km.

Schließlich kann man für Neutronensterne, auf denen einfallendes Material von einem Begleitstern nach Verdichtung und Aufheizung thermonuklear zündet und eine expandierende leuchtende Hülle (Photosphäre) erzeugt („Photospheric Radius Extension Burst“) den Radius bestimmen. Die maximale Helligkeit wird bei größter Oberfläche erzeugt, die erreicht wird, wenn der Strahlungsdruck der Explosion sich im Gleichgewicht mit der Anziehungskraft des Neutronensterns befindet. Hier geht die Masse des Neutronensterns schon mit ein. Aus der Leuchtkraft der Photosphäre konnten Feyal Özel und Paulo Freire für Neutronensterne von 1,5 Sonnenmassen einen Radius zwischen 9,9 und 11,2 km bestimmen. Drei sehr unterschiedliche Messmethoden bestätigen also, dass Neutronensterne wirklich sehr kompakte Objekte sind. Ihre Dichte ist demnach ein bis zweimal so hoch wie die von Atomkernen (ca. 300 Millionen Tonnen pro Kubikzentimeter), was somit ein Beleg dafür ist, dass sie tatsächlich aus verdichteten Kernteilchen bestehen.